ปีทาโกรัส (Pythagoras)
ปีทาโกรัส (Pythagoras) ประมาณ 572 - 500 ก่อนคริสต์ศักราช
ประวัติ
ปีทาโกรัสเป็นชาวกรีก เกิดที่เกาะซามอสใกล้กับเอเซียไมเนอร์ เนื่องจากทรราช Polycrates ท่านจำต้องออกจากเกาะซามอส กล่าวกันว่าท่านเคยศึกษาที่อียิปต์และ เป็นศิษย์ของทาลิส ปีทาโกรัสได้ก่อตั้งสำนักปิทาโกเรียน ที่เมือง Crotona ซึ่งอยู่ทางตอนใต้ของ ประเทศอิตาลี ปีทาโกรัสคิดว่าปริมาณต่าง ๆ ในธรรมชาติสามารถเขียนในรูปเศษส่วนของ จำนวนนับ จนมีคำขวัญของสำนักว่า "ทุกสิ่งคือจำนวนนับ" เมื่อมีการค้นพบจำนวนอตรรกยะขึ้น ทำให้ปีทาโกรัสและศิษย์ทั้งหลายเสียขวัญและกำลังใจ เมื่อทางราชการขับไล่เพราะกล่าวหาว่า สำนักปีทาโกเรียนเป็นสถาบันศักดินา สำนักปีทาโกเรียนก็สูญสลายไป
ผลงาน
เราไม่ทราบแน่ชัดว่าผลงานชิ้นใดเป็นของปีทาโกรัสชิ้นใดเป็นของลูกศิษย์ จึงกล่าวรวมๆ ว่าเป็นของสำนักปีทาโกเรียน ซึ่งมีดังนี้
1. จำนวนคู่และจำนวนคี่
2. ค้นพบความสัมพันธ์ระหว่างเศษส่วนกับทฤษฎีของดนตรี
3. จำนวนเชิงรูปเหลี่ยม เช่น จำนวนเชิงสามเหลี่ยม , จำนวนเชิงจตุรัส
4. จำนวนอตรรกยะ
5. พีชคณิตเชิงเรขาคณิต
6. พิสูจน์ทฤษฎีบทปีทาโกรัส
ตามที่ได้กล่าวไปแล้วข้างต้น หาก c แทนความยาวด้านตรงข้ามมุมฉาก และ a และ b แทนความยาวของอีกสองด้านที่เหลือแล้ว ทฤษฎีบทพีทาโกรัสจะสามารถเขียนในรูปสมการพีทาโกรัสได้ดังนี้
ถ้าทราบความยาวของทั้ง a และ b ค่า c จะสามารถคำนวณได้ดังนี้
ถ้าทราบความยาวด้านตรงข้ามมุมฉาก c และด้านประชิดมุมฉากด้านใดด้านหนึ่ง (a หรือ b) แล้ว ความยาวด้านที่เหลือสามารถคำนวณได้ดังนี้
หรือ
ทฤษฎีบทพีทาโกรัสกำหนดความสัมพันธ์ของด้านทั้งสามของสามเหลี่ยมมุมฉากอย่างง่าย เพื่อที่ว่าถ้าทราบความยาวของด้านสองด้าน ก็จะสามารถหาความยาวของด้านที่เหลือได้ อีกบทแทรกหนึ่งของทฤษฎีบทพีทาโกรัสคือ ในสามเหลี่ยมมุมฉากใด ๆ ด้านตรงข้ามมุมฉากจะยาวกว่าสองด้านที่เหลือ แต่สั้นกว่าผลรวมของทั้งสอง
ทฤษฎีบทดังกล่าวสามารถกล่าวโดยสรุปได้เป็นกฎของโคซายน์ ซึ่งเมื่อให้ความยาวของด้านทั้งสองและขนาดของมุมระหว่างด้านนั้นมา จะสามารถคำนวณหาความยาวด้านที่สามของสามเหลี่ยมใด ๆ ได้ ถ้ามุมระหว่างด้านเป็นมุมฉาก กฎของโคซายน์จะย่อลงเหลือทฤษฎีบทพีทาโกรัส
บทกลับของทฤษฎีบทปีทาโกรัสนั้นเป็นจริง โดยกล่าวไว้ดังนี้
กำหนด a, b และ c เป็นจำนวนจริงบวกที่จะมีสามเหลื่ยมมุมฉากหนึ่งรูปที่มีความยาวด้านเท่ากับสามจำนวนนั้น และสามเหลี่ยมนั้นจะมีมุมฉากระหว่างด้าน a และ b
สำหรับสามเหลี่ยมใด ๆ ที่มีด้าน a, b และ c ถ้าแล้วมุมระหว่าง a กับ b จะวัดได้ 90°
ถ้าในสามเหลี่ยมรูปหนึ่ง สี่เหลี่ยมบนด้านหนึ่งเท่ากับผลรวมของสี่เหลี่ยมบนอีกสองด้านที่เหลือของสามเหลี่ยมแล้ว แล้วมุมที่รองรับด้านทั้งสองที่เหลือของสามเหลี่ยมนั้นจะเป็นมุมฉาก
กำหนดสามเหลี่ยม ABC มีด้านสามด้านที่มีความยาว a,b และ c และ  เราจะต้องพิสูจน์ว่ามุมระหว่าง a และ b เป็นมุมฉาก ดังนั้น เราจะสร้างสามเหลื่ยมมุมฉากที่มีความยาวของด้านประกอบมุมฉาก เป็น a และ b แต่จากทฤษฎีบทปีทาโกรัส เราจะได้ว่าด้านตรงข้ามมุมฉาก ของสามเหลื่ยมรูปที่สองก็จะมีค่าเท่ากับ c เนื่องจากสามเหลี่ยมทั้งสองรูปมีความยาวด้านเท่ากันทุกด้าน สามเหลี่ยมทั้งสองรูปจึงเท่ากันทุกประการแบบ "ด้าน-ด้าน-ด้าน" และต้องมีมุมขนาดเท่ากันทุกมุม ดังนั้นมุมที่ด้าน a และ b มาประกอบกัน จึงต้องเป็นมุมฉากด้วย
เราจะต้องพิสูจน์ว่ามุมระหว่าง a และ b เป็นมุมฉาก ดังนั้น เราจะสร้างสามเหลื่ยมมุมฉากที่มีความยาวของด้านประกอบมุมฉาก เป็น a และ b แต่จากทฤษฎีบทปีทาโกรัส เราจะได้ว่าด้านตรงข้ามมุมฉาก ของสามเหลื่ยมรูปที่สองก็จะมีค่าเท่ากับ c เนื่องจากสามเหลี่ยมทั้งสองรูปมีความยาวด้านเท่ากันทุกด้าน สามเหลี่ยมทั้งสองรูปจึงเท่ากันทุกประการแบบ "ด้าน-ด้าน-ด้าน" และต้องมีมุมขนาดเท่ากันทุกมุม ดังนั้นมุมที่ด้าน a และ b มาประกอบกัน จึงต้องเป็นมุมฉากด้วย
 เราจะต้องพิสูจน์ว่ามุมระหว่าง a และ b เป็นมุมฉาก ดังนั้น เราจะสร้างสามเหลื่ยมมุมฉากที่มีความยาวของด้านประกอบมุมฉาก เป็น a และ b แต่จากทฤษฎีบทปีทาโกรัส เราจะได้ว่าด้านตรงข้ามมุมฉาก ของสามเหลื่ยมรูปที่สองก็จะมีค่าเท่ากับ c เนื่องจากสามเหลี่ยมทั้งสองรูปมีความยาวด้านเท่ากันทุกด้าน สามเหลี่ยมทั้งสองรูปจึงเท่ากันทุกประการแบบ "ด้าน-ด้าน-ด้าน" และต้องมีมุมขนาดเท่ากันทุกมุม ดังนั้นมุมที่ด้าน a และ b มาประกอบกัน จึงต้องเป็นมุมฉากด้วย
เราจะต้องพิสูจน์ว่ามุมระหว่าง a และ b เป็นมุมฉาก ดังนั้น เราจะสร้างสามเหลื่ยมมุมฉากที่มีความยาวของด้านประกอบมุมฉาก เป็น a และ b แต่จากทฤษฎีบทปีทาโกรัส เราจะได้ว่าด้านตรงข้ามมุมฉาก ของสามเหลื่ยมรูปที่สองก็จะมีค่าเท่ากับ c เนื่องจากสามเหลี่ยมทั้งสองรูปมีความยาวด้านเท่ากันทุกด้าน สามเหลี่ยมทั้งสองรูปจึงเท่ากันทุกประการแบบ "ด้าน-ด้าน-ด้าน" และต้องมีมุมขนาดเท่ากันทุกมุม ดังนั้นมุมที่ด้าน a และ b มาประกอบกัน จึงต้องเป็นมุมฉากด้วย
จากบทพิสูจน์ของบทกลับของทฤษฎีบทปีทาโกรัส เราสามารถนำไปหาว่ารูปสามเหลี่ยมใด ๆ เป็นสามเหลี่ยมมุมแหลม, มุมฉาก หรือ มุมป้าน ได้ เมื่อกำหนดให้ c เป็นความยาวของด้านที่ยาวที่สุดในรูปสามเหลี่ยม
- ถ้า
 สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมฉาก
สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมฉาก - ถ้า
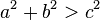 สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมแหลม
สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมแหลม - ถ้า
 สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมป้าน
สามเหลี่ยมนั้นจะเป็นสามเหลี่ยมมุมป้าน
ที่มาวีดีโอ http://www.youtube.com/watch?v=jlOB4OFhGsw 14 กันยายน 2556







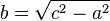
Slots for hire | Slot Machine | JtmHub
ตอบลบJtm is the leading 문경 출장마사지 iGaming company, 오산 출장샵 founded in 2012, and 상주 출장안마 now we've added a few 춘천 출장샵 new and emerging software companies like Slots. 계룡 출장샵